본문영역
|
이 세상은 내가 생각하는것보다 훨씬 복잡하다
Birthday Paradox - 방안의 36명 중 같은 생일을 가진 사람이 있을 확률은?
2008-11-10 19:28:35최종 업데이트 : 2008-11-10 19:28:35 작성자 : 시민기자 송인혁
|
||||||||||||||||||||||||
|
먼저 질문을 하나 던지겠습니다.
방안에 36명이 있습니다. 누군가를 기다리고 있는 중이었죠.
그런데 기다리고 있던 한 사람이 지루해서 엉뚱한 내기를 제안합니다.
"심심한데 게임이나 합시다~
우리 중에서 생일이 같은 사람이 있을까요, 없을까요! 저는 없다에 한표!"
다소 생뚱맞게 내기 게임을 제안합니다. 36명 중에 같은 생일을 가진 사람이 있을까요?없을까요? 확인해보기 전에는 절대 알 수 없는 노릇이지만... 같은 생일을 가진 사람이
있을 확률은 얼마나 될까요?
저는 처음 이 질문을 들었을 때, '없을 확률이 많다'에 걸었습니다. 1년이 365일인데,
방안에는 36명이니... 골고루 생일이 분포되어 있다고 가정해도... 36/365 = 10% 잖아요.
여러분은 어떻게 생각하세요?
계산까지는 아니더라도 걍 없을 것 같은 느낌이에요? 있을 것 같다는 느낌이에요?
대부분의 사람은 '없을 것 같다'에 한표를 던집니다. 그러나 사실은 '있을 가능성이 높다'가 정답입니다. 그것도 매우 높은 확률로!! 에에? 뭔가 질문한 의도로 봐서 '있을 확률이 높다'가 정답이겠지라고 짐작하신 분도 아리송 할 것입니다.
어째서 이런 일이 벌어지는걸까요?
우리의 직관이 이리도 보기좋게 틀려버리는걸까요.
비밀은 간단합니다.
'나와 다른 사람들간의 관계만 생각'하기 때문입니다. 그리고 '나'를 사람들의 가운데에 두려는 성향 때문이지요. 36명의 사람이 있는데, 36/365 정도의 확률을 떠올리는 것은... 나와 나머지만 비교했을 때 얘기입니다. 방에는 나와 누군가와의 관계만 있는게 아니라, 누군가와 다른 누군가와의 관계도 있다는 거... 아직 이해 안되시는 분을 위해... 정말 그런지를 살펴보도록 하지요. 1. 두 사람 사이 :
두 사람의 생일이 같은 확률은 1/365입니다. 한번만 비교하면 되니까요. 같거나 다르거나~ 그렇죠? 2. 세 사람 사이 : 세 사람에서는 몇번 비교를 해야 할까요? 두번 비교를 하게 될까요? 아니죠. 나와 나머지 두 사람, 그리고 저 아래의 나머지 두 사람끼리의 관계. 이렇게 세번입니다.
3. 네 사람은요? 네번째 비교에서부터는 보다 눈에 띄는 모양새가 생겨납니다. 나와 나머지 세 사람간의 관계, 세번 비교를 하게 되죠. 그리고 옆에 있는 사람과 나머지의 관계 (2번), 그리고 또 나머지와의 관계(1번). 이렇게 해서 모두 6번의 비교를 하게 됩니다. 그래서 방안에 네명만 있어도 4번의 비교가 아니라 6번의 비교를 하게 됩니다. 5명이면? 10번입니다. 6명이면? 15번! 10명이면? 45번~ 경우의 수를 죽 계산해 보면, 금방 아래와 같은 형태의 기하급수임을 눈치채실 것입니다. 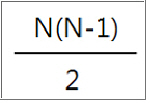 이 세상은 내가 생각하는것보다 훨씬 복잡하다_1 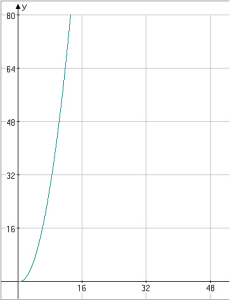 이 세상은 내가 생각하는것보다 훨씬 복잡하다_2 비교의 횟수는 이만큼 된다는 것이구요,
그럼, 실제 동일한 생일이 없을 '확률'은 얼마나 될까요? 공식적으로는 쪼금 복잡합니다. 다소 약식으로 계산하는 공식을 보여드리면... 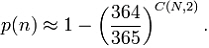 이 세상은 내가 생각하는것보다 훨씬 복잡하다_3 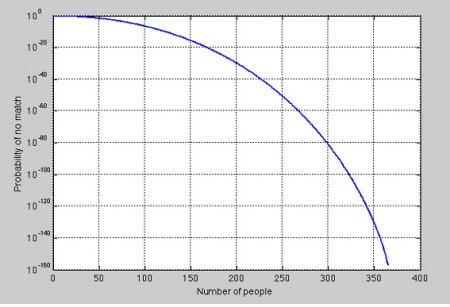 출처: http://en.wikipedia.org/wiki/Birthday_paradox 사람 숫자당 확률을 도표로 나타내보면 아래와 같습니다.
그래프에 따르면, 23명만 넘어가면 같은 생일이 있을 확률은 50%가 넘어갑니다. 오호라~~~ 만약 57명이 넘으면 99%인거죠. 비교횟수는 장난 아니겠죠? ^^ 어떻습니까~ 이것이 바로 Birthday Paradox 라는 현상입니다. 혹시 사람들이 30명 넘게 모여있는 경우가 있다면, 이런 패러독스를 실험해 보는 것도 재미있을 것 같아요!! 물론, 확률이기 때문에 동일한 생일을 가진 사람이 없을 수도 있습니다. 허나 있을 가능성은 정말 높습니다. 그래서 뭐? 사람들이 좀 많으면, 생일이 같을 확률이 내가 생각했던 것보다 좀 더 많다는게 어쨌다고? 라고 생각하실 수도 있습니다. 우리가 관심을 가져야 할 점은 바로 이것입니다. 우리가 사회를 바라보는 관점 역시 이와 다르지 않다는 것이죠. 이 세상은 나와 내가 아닌 누군가와의 관계로만 이루어져 있지 않습니다. 나와 누군가와의 관계와 마찬가지로 다른 누군가와 또 다른 누군가와의 관계 역시 마찬가지로 존재한다는 점입니다. 그 관계의 숫자가 조금만 커져도 방금전에 그래프를 통해 설명드린 것처럼 우리의 예상을 훨씬 뛰어넘는 정도의 복잡성을 가지게 되는 것입니다. 이 사회는 그래서 우리가 생각하는 것 이상으로 수많은 다양성과 복잡한 관계로 얽히고 섥혀 있는 것입니다. 때문에 오늘 하루를 살아가는 우리들이 Birthday Paradox에서 저지른 실수처럼, 자칫 나의 잣대로 타인을 평가하고만 있지는 않은지... 그 사람의 세상이 나와 다를 수 있음을 묵과하고 있는건 아닌지, 다른 가치를 가지는 세상을 애써 내가 무시하고 있는건 아닌지 생각을 해 보아야 하지 않겠습니까 ^^ 그런걸 생각하는 하루가 되었으면 좋겠습니다. 연관 뉴스
|
||||||||||||||||||||||||
많이 본 뉴스
- [장안구] "만석공원의 낮과 밤을 함께 즐겨요" 만석거 새봄 페스타 19~20일 개최
- '2024년 수원팔색길걷기 행복여행' 1색 모수길은 '야생화 꽃길'
- "수원에 초등 대안학교가 있어요"
- 수원시 송정초, 신나고 재미 있는 '송정 과학 축제의 날' 행사 개최
- 수원시, 2024년 임신 사전 건강관리 검사비 지원
- 중등수원칠보산자유학교, 개교 10주년 행사 열려
- 수원시, 수원연극축제 주제공연 '울림' 시민공연자 모집
- 만석공원을 거닐며 시각 예술가 최경아와 함께하는 참여형 예술 워크숍
- 치매 예방을 위한 음악 모임 프로그램 '즐거운 힐링멜로디'
- '2024 만석거 새빛축제' 불꽃놀이쇼 19일로 변경
 즐겨찾기 추가
즐겨찾기 추가